How do teachers help their students become active math learners?
During large groups lessons, students are passive learners, even if they are learning by listening, and viewing an example. Yet they are not active math learners until they start “doing” the math.
I propose a change. Every grade level K-8th and even high school should introduce each new math concept with a hands-on activity that each student must do. The teacher should not explain the whole process, but show the math concepts and then ask the students what they know about it. Also ask the students what part is confusing to them. Students who can do either of these are already analyzing the math concept. When teachers continue to introduce concepts in this manner, students become used to thinking about math, connecting with their prior knowledge, and communicating their thinking or questions.
Why? The answer is because the students become active math learners from the very beginning! Think back to your years working on math as a student, especially in high school. Even if you were able to focus during the 20 minute lecture explaining the formulas, you didn’t begin to understand the concept until you tried using it. Then you would think of all kinds of questions and/or become stuck.
Students who begin to manipulate :
1. the math concepts with ten frames begin to visually see the concept of 5 plus one more.
2. ten frames mats to begin to visually see the concept of comparing numbers.
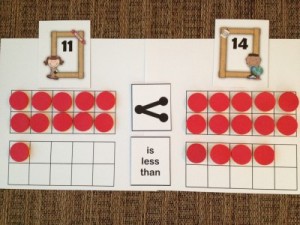
Guided Math First Grade Place Value Activities using ten frame comparing to become active math learners
3. base ten units on a tens and ones chart begin to visually see the concept of regrouping in addition or subtraction.
4. red/yellow counters into rows and columns of an array begin to visually see the concept of multiplication or repeated addition.
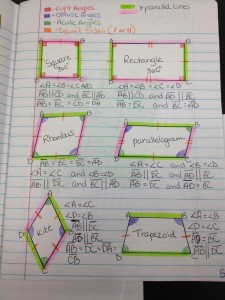
5. rubber bands on a geoboard begin to visually see the different quadrilaterals and their similarities or differences.
6. fraction towers begin to visually see the concept of addition of fractions with unlike denominators.
7. algebra tiles begin to visually see the concept of solving equations for x and/or y.
These hands-on activities that help students visualize the concept are the concrete method of teaching. From these activities teachers can build math comprehension by making connections between what the students did and showing the students the abstract math concept.